20世纪40年代，采用玻璃纤维制成的滤料开始出现；20世纪50年代，非织布滤料在国外迅速发展时，我国还停留于以机织物为主的过滤材料上；20世纪70年代后，我国非织布滤料开始发展起来，当时主要采用的是化学粘合和湿法的方法，而不是采用熔喷技术。熔喷法可以产生超细纤维（0.5～10 μm），因此具有更大的比表面积和孔隙率。

 

对于同种滤料不同结构参数的过滤特性，国内外学者做了很多研究。肖慧明等测定了熔喷聚丙烯驻极体空气过滤材料对离子型（KCL）、极性非离子型（DEHS）2种不同试验气溶胶粒子的粒径、荷电特性及流动速率对过滤性能的影响［1］。袁传刚等研究了熔喷法聚丙烯过滤材料加工工艺参数对其性能的影响［2］。李柏松等通过理论计算的方法，研究了过滤材料的结构参数改变对过滤效率的影响［3］。陈乐瑞等通过建立二维模型，模拟计算了在不同运行工况下，纤维过滤器的压力损失和对不同粒径范围内的颗粒物过滤效率［4］。付海明等通过模拟的方法，研究了纤维间距和风速等参数的改变对滤料过滤性能的影响［5，6］。冯朝阳等通过试验测试了不同结构参数核级高效空气过滤器的阻力，对过滤器的结构与其阻力之间的关系进行了分析［7］。吴利瑞等首先分析了滤筒的直径、褶间夹角、褶数和褶高之间的关系［8］。巴鹏等首先利用理论分析方法建立滤芯结构参数和阻力之间的数学模型，然后根据计算获得的经验公式拟合出了褶间夹角褶高阻力的关系曲面图［9，10］。Chen等利用有限元法对型平板状褶式滤芯进行了数值模拟研究［11，12］。Subrenat等通过建立单个褶的三维模型对种结构参数的圆筒状褶式滤芯进行了流场模拟［13］。TOBIAS等开发模型对褶皱的几何形状和过滤性能进行尺寸优化设计［14］。Stef fens等分析了同构和异构两种纤维模型［15，16］。S Fotovati等建立了一个宏观模型来模拟深褶过滤器的瞬时采集效率和压降以及粉尘负荷褶皱过滤器压降的影响［17，18］。V Nassehi等结合单孔或多孔流动的有限元建模，通过褶筒流场模拟过滤器的性能。

 

综上所述，现有研究虽然能反映出相关结构参数和运行条件对滤芯阻力及过滤效率的影响趋势，但仍存在一些不足之处：各结构参数对过滤效率及阻力影响的研究都是以其他结构参数及过滤速度固定为前提，缺少各因素综合影响下的过滤效率和阻力变化情况，无法比较各因素对过滤效率及阻力影响的显着性。本文采用熔喷聚丙烯材料制作褶皱过滤器，以固定过滤介质的褶式滤芯为研究对象，通过试验测试褶深度、褶间距及风量等因素对滤芯过滤效率及阻力的影响进行研究，总结各因素对过滤效率及阻力的影响趋势和显着性，所得结果对优化褶式滤芯的结构设计有重要的理论价值和现实意义。

 

2 褶皱过滤器试验装置及条件

2.1 试验装置

试验装置主要包括以下4个部分：风管系统、测量系统、动力装置和采样装置等组成，如图1所示。

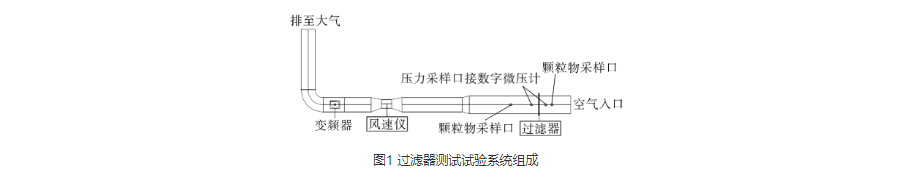
（1）风管系统：风管采用2 mm镀锌钢板制成，其断面尺寸为610 mm×610 mm。系统采用负压吸入式，驱动的风机系统安装在系统后侧，过滤后的空气排到大气中，从空气入口到空气出口各段按照功能依次为：进风段、过滤段、流量测试段和排风段。

（2）测量系统：经过过滤器前后的气溶胶中颗粒物浓度采用Met OneA 2400型激光粒子计数器测得，阻力DP1000-II采用数字微压计测得。

（3）动力系统：采用变频器和离心风机作为动力系统。

（4）采样系统：采样管与激光粒子计数器之间采用软管连接，激光粒子计数器的采样管位于管道的中心位置。

 

2.2 试验条件

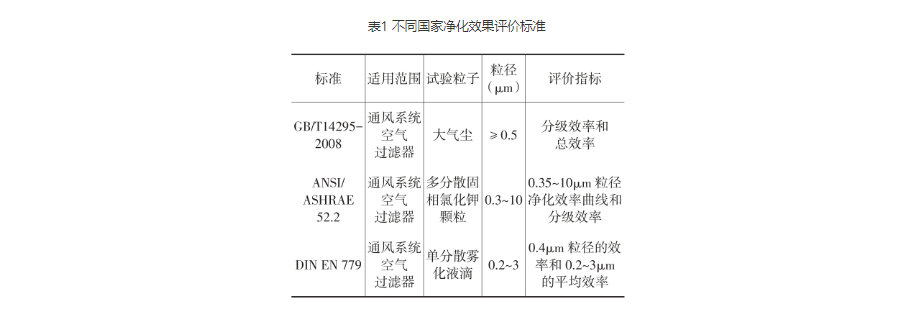
本次试验采用的测试尘源为环境气溶胶（大气尘），不同国家净化效果评价标准见表1。在一定的滤速下，将环境气溶胶抽入管道内部，含尘气流中的颗粒物在流经过滤材料时会被拦截，通过测量测试前后颗粒物的数量就可以计算出该过滤器的过滤效率。然后通过数字微压计测量不同风速下过滤器前后的静压差，即为过滤器的阻力。

系统的洁净程度对试验结果有直接影响，为使试验数据准确，因此在每次测量前和每改变一次风量时，使用高压氮气进行25～30 min的吹气，去掉风道和过滤器上残留的粉尘。为了提高试验条件，打开电源，调试激光粒子计数器，每次测定包括10个30 s的周期，间隔时间是5 s。打开运行开关，观察计数器的计数的变化。观察可知，当达到一定程度时，将稳定在一个很小的变化范围内，此时粒子的数量基本都为十位甚至个位数，即可进行测试。

 

3 褶皱过滤器效率试验结果及分析

褶皱过滤器具有过滤面积大，过滤效率高，使用寿命长等特点，与其他形式的过滤器相比，在技术上和经济上更适用于对室内颗粒物的控制。本文选取几种不同褶深度和褶间距组合的过滤器进行试验，分别测试出其在不同风速下的过滤效率和阻力，通过对实验数据的分析，得出不同过滤器结构参数下的过滤效率性能曲线和阻力特性曲线，讨论分析了褶深度和褶间距两种因素的改变对过滤器性能的影响。

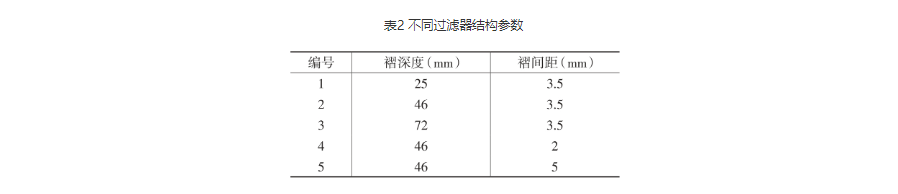
本试验测试选用的过滤器尺寸为610 mm×610 mm，各测试对象的褶间距和褶深度见表2。

 

3.1 褶深度对过滤效率的影响

褶深度对不同粒径颗粒过滤效率的影响如图2所示。

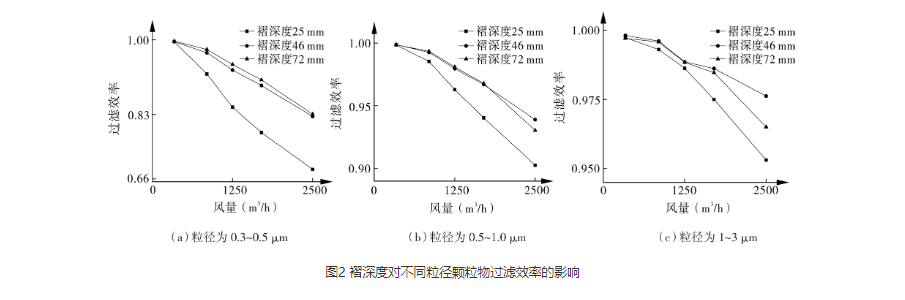
从图2中可以看出，在不同粒径范围内，风量越小，褶皱过滤器过滤效率越高。当粒径直径小于0.5 μm时，褶深度为72和46 mm的过滤器效率较为接近，但都高于褶深度为25 mm的过滤器；对于颗粒物直径在0.5～1.0 μm范围内，褶深度为72和46 mm的过滤器，随着风量的增加，过滤效率下降较为平缓；对于颗粒物直径为1～3 μm的粒子，褶深度为46的过滤器过滤效率要高于深度为72 mm的过滤器，同时两者在各风速下的过滤效率均高于褶深度为25 mm的过滤器；对于颗粒直径为0.3～3 μm的粒子，当风量为340 m3/h时，三者的过滤效率基本相同，随着风量的增加，3种褶深度的过滤器过滤效率一直下降。

 

分析这种差别的产生可能与制成过滤器的材料本身过滤特性有关，风量越小，褶皱过滤器的过滤效率越高。这是因为在风量下，小颗粒的扩散作用明显，气流在过滤介质中滞留的时间较长，颗粒物有更多的机会撞击障碍物。虽然此时粒径大的颗粒在惯性运动时与纤维碰撞的机率减小，但是在实际应用中这种影响并不明显，因为风量减小了，纤维对颗粒物的反弹力也减小了，颗粒物更容易粘附，过滤效果明显提高。但在一定程度上增大过滤器的褶深度能提高过滤性能的稳定性，这是因为在褶间距不变的情况下，增大过滤器的褶深度，使得含尘气流在过滤器内的紊乱程度增加，停留时间增长，使得扩散作用增强，而扩散作用主要提高了小粒径颗粒物的过滤效率，而随着颗粒物直径的增加，扩散作用逐步减弱，拦截和惯性效应逐渐增加。因此，随着褶深的增大，通过褶两端区域的气流越少，通过褶中部区域的气流越多，即随着的增大褶通道内的气流分布越不均匀，这也可能是造成过滤器过滤效率降低的原因［20］。

 

3.2 褶间距对过滤效率的影响

从图3中可以看出，在过滤器褶深度一定的情况下，并不是褶间距越小过滤效果越好。在不同粒径范围内，褶间距为3.5 mm的过滤效率均大于褶间距2和5 mm的过滤效率。当粒径小于0.5 μm时，褶间距2和5 mm的过滤器，其过滤效率随风量变化的趋势相似，两者效率均低于褶间距为3.5 mm的过滤效率，并且随着风量的增加，过滤效率的差距越大；而对于粒径为0.5～1.0 μm的粒子，随着风量的增加，三者变化趋势相似但过滤效率在数值上有所差别，其中褶间距为3.5 mm过滤器的过滤效率最高；当粒径在1～3 μm范围内，褶间距为2和3.5 mm的过滤效率变化趋势较为相似，且两者的效率均大于褶间距为5 mm的过滤效率。

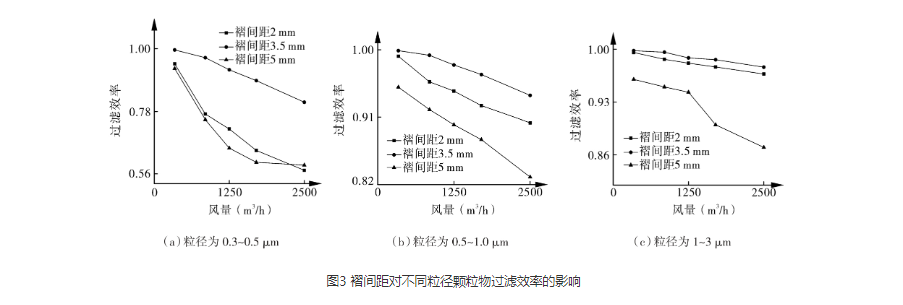
从上述分析可以得出，随着褶间距的增大，过滤效率呈现先增大后减小的趋势，也就是说存在一个褶间距，在该间距下，同种材料制成的过滤器过滤效率将达到最大。理论上来说，褶间距越小，过滤材料将用的越多，过滤性能越好。但这种情况是将过滤过程看作一个静态过程，并没有考虑被纤维过滤器捕集的颗粒物再次被气流吹离的情况。随着过滤器褶间距减小，含尘气体变得更加紊乱，气流分布不均匀，颗粒物的扩散作用将会提高，过滤效率将会增大。当气流变得更加紊乱时，已经被吸附到纤维表面的颗粒物将重新穿透过滤器，从而使得整体过滤效率降低；而当褶间距增大时，褶间距内气流相互影响越来越弱，几乎不会增加含尘气流的紊乱程度，从而使得过滤器过滤效率更加接近于单层过滤材料本身的过滤效率。过滤器的过滤效率在流动不均匀和流动均匀两种情况下有很大差别，且流动越均匀，过滤器过滤效率越高［21～23］。因此，在不同粒径下，不同褶间距的过滤器会出现以上变化趋势。

 

4 褶皱过滤器阻力试验结果及分析

用单层过滤材料制作褶皱过滤器，其阻力主要由3个部分组成：滤料本身阻力、进出口阻力和结构阻力。过滤器进出口阻力一般是一个变化不大的定值，可以作为过滤器的定值附加在计算结果中。对于过滤器而言，过滤材料本身阻力是气流通过纤维材料时，其迎面阻力造成的，其数值大小与纤维材料本身结构性质有关；其结构阻力与褶深度和褶间距有关。

 

4.1 褶深度对过滤阻力的影响

褶深度对过滤器阻力的影响如图4所示。

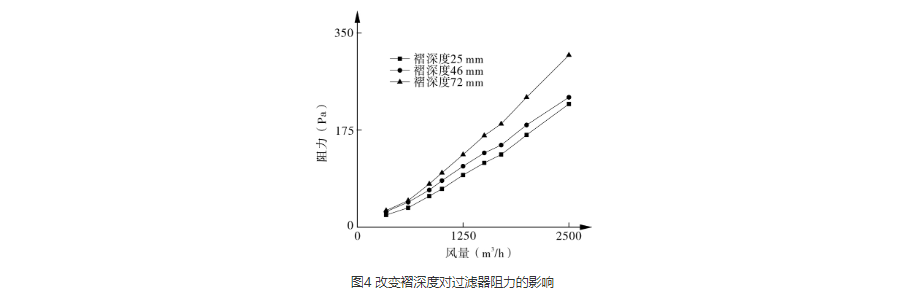
从图4可以看出，随着风量增加，过滤器阻力呈现增大趋势，且褶深越大，过滤器的阻力越大。在实际工程应用中，过滤器的设计人员只关注过滤器断面尺寸、额定通风量和阻力，在很多情况下对褶皱过滤器的褶深度没有严格要求。尽管增加褶皱过滤器的褶深度会造成过滤器阻力的增加，但在实际应用中，还应该考虑减小褶深对过滤效率及过滤强度的影响。褶皱过滤器的褶深度还受折叠工艺和滤料自身强度的影响，当褶深度太小时，会降低过滤器的结构强度，使其抗气流冲击能力下降，不能在较大风量下运行。在确定褶深度时，还要考虑其过滤效率的影响，结合上文改变褶深对过滤效率的影响分析，当褶深度为46 mm时，过滤效率较高（大于0.5 μm颗粒物的过滤效率均达到90%），其阻力比褶深为72 mm阻力低（最大阻力低32%）。

 

4.2 褶间距对过滤阻力的影响

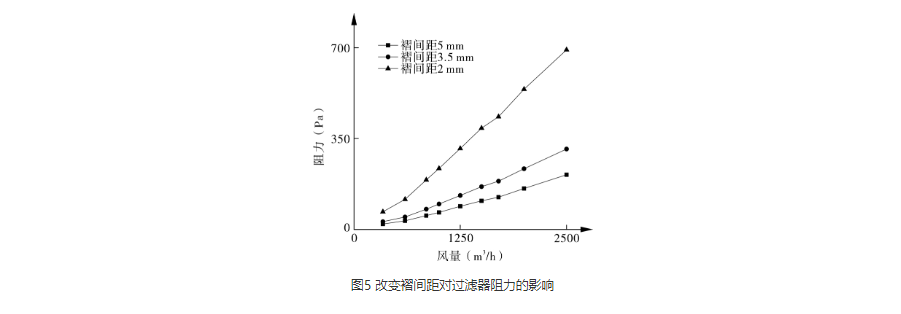
在过滤器尺寸确定的情况下，减小过滤器褶间距，可以有效增加过滤器滤料面积，从而在风量一定情况下，可以有效减小滤速。从图5可以看出，随着风量增加，过滤器阻力均出现增大趋势，且褶间距越小，阻力越大。从数值上看，当风量为1000 m3/h时，间距从3.5 mm增大到5 mm，阻力从89 Pa增加到131 Pa，增幅为47%；而从2 mm增大到3.5 mm时，阻力从131 Pa增加为312 Pa，增幅为138%。尽管增加褶间距间隔相同，但阻力差别很大，因此可以预测，随着褶间距减小，阻力增幅将越来越大。这可以说明，减小褶间距可增加过滤面积，减小滤速，但随着褶间距减小，气流通道将会变窄，增大了气流在过滤器内的扰动程度，从而增加了气流在通道内的能量损失，使得通过减小滤速来减少的阻力远远小于减少褶间距造成通道内的阻力损失，这种改变得不偿失。

因此，在设计过滤器时，需考虑以上2种因素的共同作用，在选择过滤器褶间距时会有一个较合适的范围。在实际应用中，褶间距过大会影响过滤器结构，而过小会造成阻力增速很大；在选择褶间距时还要同时考虑对过滤性能的影响。结合对过滤效率的分析，选择褶间距为3.5 mm较为合适，在此条件下，对于粒径大于0.3 μm的颗粒物，过滤效率均可以达到90%，与此同时，其阻力损失也在可以接受范围内。

 

5 结论

（1）对于粒径小于1 μm的颗粒物，增加过滤器的褶深度，总体上会使过滤器的过滤效率提高，但随着颗粒物直径的增加大于1 μm时，褶深度对提高过滤效率的这种优势将会消除。

（2）在褶皱过滤器褶深度一定的情况下，不同颗粒物直径范围内，随着风量增加，褶间距为3.5 mm的过滤效率均大于褶间距为2和5 mm的过滤效率。

（3）当褶深度为46 mm时，过滤效率较高（大于0.5 μm颗粒物的过滤效率均达到90%），其阻力比褶深为72 mm阻力低（最大阻力低32%）。

（4）褶皱过滤器选择褶间距为3.5 mm，褶深度为46 mm，此时过滤性能最佳。